Modelizado experimental

Tareas

1. Subir el código Arduino lazo_abierto a la maqueta.
2. Realizar un condicionamiento de los datos tomados en el colab.
3. Identificar la función de transferencia a partir de la gráfica de los datos tomados.
4. (opcional) Identificar la función de transferencia del sistema, utilizando la aplicación de Matlab llamada System Identification.

Descripción de la planta

La planta es un sistema de iluminación con un LED de potencia (actuador) y un LDR (sensor). Este sistema es controlado a través de un Arduino X. A continuación se presenta una imagen del sistema:

Ejecución

Para desarrollar este laboratorio seguiremos cada una de las tareas de forma secuencial.

1. Subir el Código Arduino

Abramos el archivo control_iluminacion en el Arduino IDE. Para ubicar el puerto de comunicación serial vamos al menú Herramientas > Puerto. Seleccionamos el puerto donde se encuentre el Arduino X.

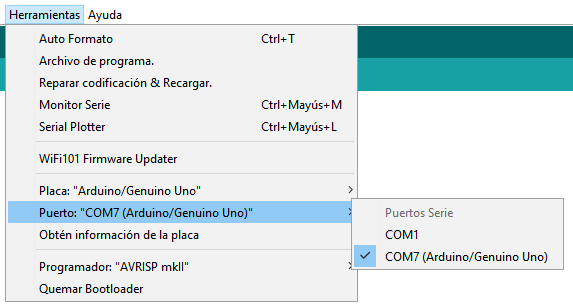
Verificamos en la maqueta donde se tiene conectada la entrada y la salida. Y corregimos los pines en el código.

#define OUT 2
#define IN A0

Luego, subimos el código al Arduino X.

Este código básicamente lee la información del sensor y la envía por puerto serial al computador, esta información esta codificada en código ASCII. Adicionalmente si uno envía un valor (0-255) por el puerto serial al Arduino, este cambiará la intensidad del LED proporcionalmente a este valor.

Una vez subido el código al Arduino se puede verificar vía el Monitor Serie la recepción de caracteres ASCII, enviando cualquier carácter, el carácter recibido debería cambiar.

2. Condicionamiento de Datos

Antes de identificar la función de transferencia del sistema, debemos realizar un condicionamiento de los datos. Para esto vamos a extraer los vectores tiempo, entrada y salida de la variable data. La extracción la haremos ejecutando en Matlab los siguientes comandos.

tiempo  = data.time;
entrada = data.Data(:,2);
salida  = data.Data(:,1);

Podemos verificar que hemos extraído correctamente los datos usando el comando plot(tiempo,entrada,tiempo,salida).

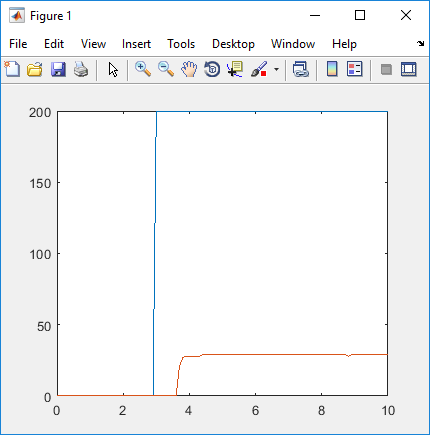
Como se puede observar la salida tiene un off-set, que debe ser eliminado para la correcta identificación del modelo. Una forma de eliminar este off-set puede ser simplemente eliminando el valor inicial de la señal de salida a todo el vector. salida = salida - salida(1). Después de este proceso, las señales quedan como se muestra a continuación.

3. Identificación del Sistema Manual

Con la figura obtenida anteriormente vamos a identificar el modelo del sistema (plot(tiempo,entrada,tiempo,salida)).

Para esto debemos definir si es un sistema de primer o segundo orden, o si es un sistema de orden superior.

Recordemos que en sistemas reales existe el retardo $\theta$ este retardo aparece por las dinámicas de los sistemas. En la función de transferencia aparece como un exponencial.

Una vez hayamos identificado el sistema vamos a identificar los parámetros del sistema para cada modelo. Recordemos que un sistema de primer orden tiene dos parámetros $\gamma$ y $\tau$ y un sistema de segundo orden tiene tres parámetros $\gamma$, $\xi$ y $\omega_n$. Y adicionalmente para cada uno el retardo $\theta$.

En el caso de ser un sistema de primer orden. Verifiquemos la cercanía del modelo evaluándolo.

s = tf('s');

gamma = 0.145;
theta = 0.6;
tau   = 0.08;

G = gamma*exp(-theta*s)/(1+tau*s)

simulacion = lsim(G,entrada,tiempo);
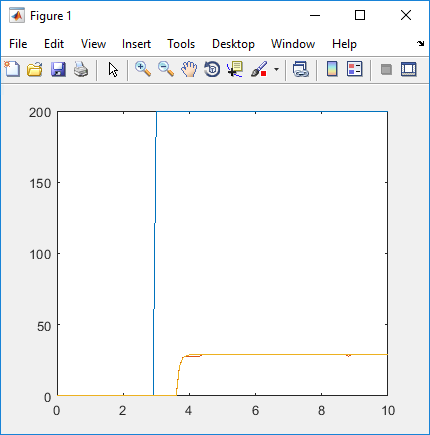
plot(tiempo,entrada,tiempo,salida,tiempo,simulacion)

Este ejemplo es para los datos del archivo modelizado.mat

4. Identificación del Sistema con el System Identification

Para una identificación automática se usará la aplicación de Matlab: System Identification.

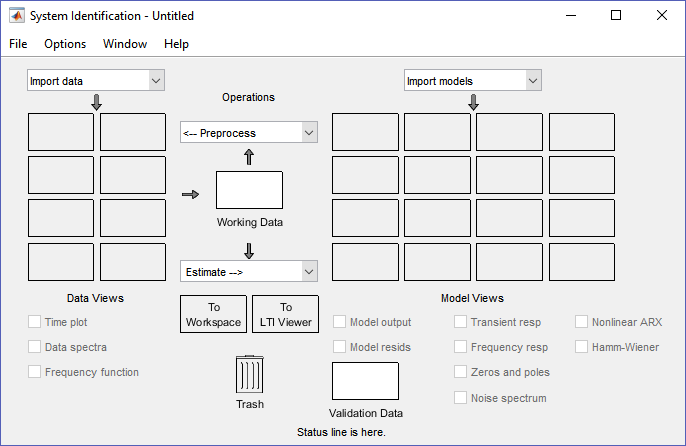
Lo primero que se debe hacer es importar los datos, para esto usaremos el menú desplegable import data y en este seleccionamos Time domain data...

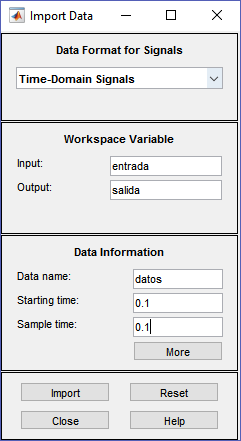
Aquí, escribiremos el nombre de las variables entrada en Input y salida en Output. Igualmente, tenemos que ingresar la información del tiempo Starting time que puede ser 0 y el Sample time que es el tiempo de muestreo (usando tiempo(2)-tiempo(1) podemos obtener este valor). Finalmente presionamos import.

Luego de la importación, haremos la identificación, para esto vamos al menú desplegable Estimate y selecionamos Process models...

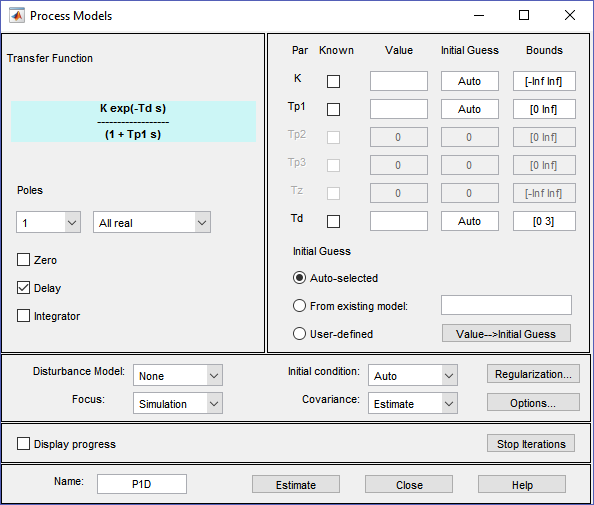
En esta ventana solo necesitamos presionar Estimate, y cerramos esta ventana. En la ventana principal, podemos verificar si el modelo representa bien la realidad seleccionando model output, esta acción abrirá una ventana donde podemos ver el ajuste.

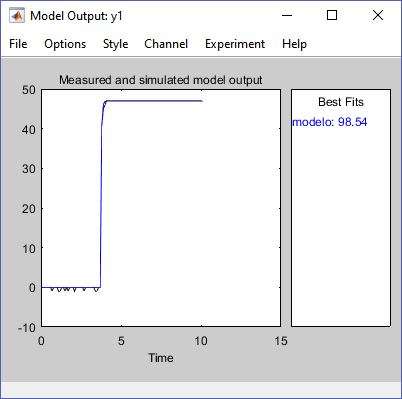
Cuando tengamos un modelo satisfactorio. Podemos arrastrar el modelo al workspace.

5. Diseño del Controlador

Para el controlador se usará la aplicación de Matlab: PID Tuner.

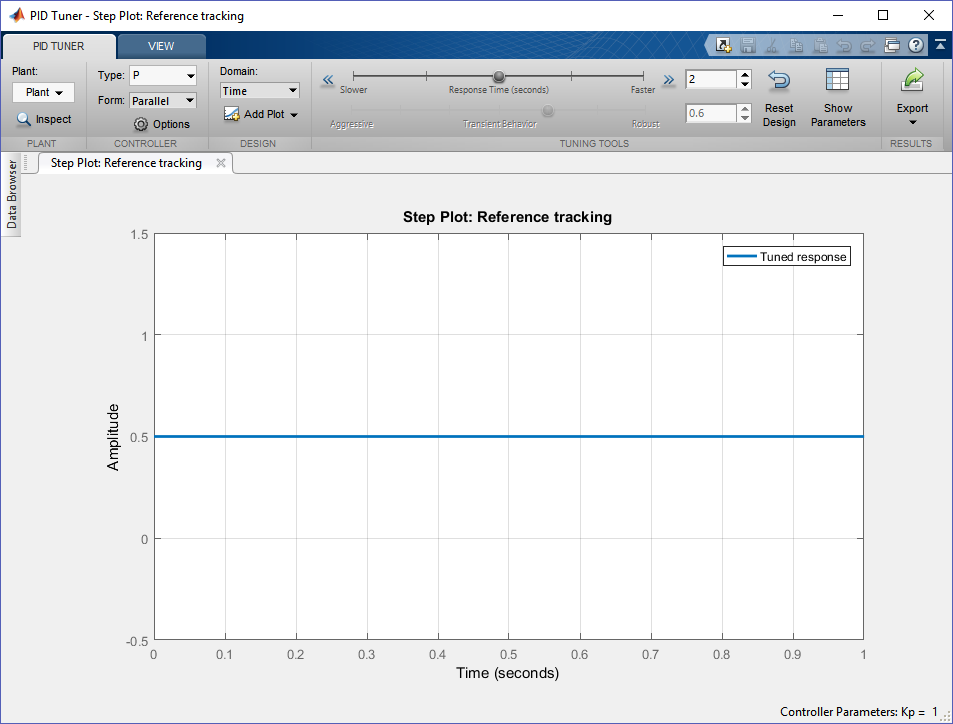
Lo primero que se debe hacer en esta ventana es importar el modelo del la planta. Para esto iremos al menú desplegable Plant > Import. Aquí seleccionaremos la variable del workspace del modelo.

Esta aplicación ofrece diferentes tipos de controladores. Para esta práctica usaremos un PID. En el menú desplegable Type selecionemos PID.

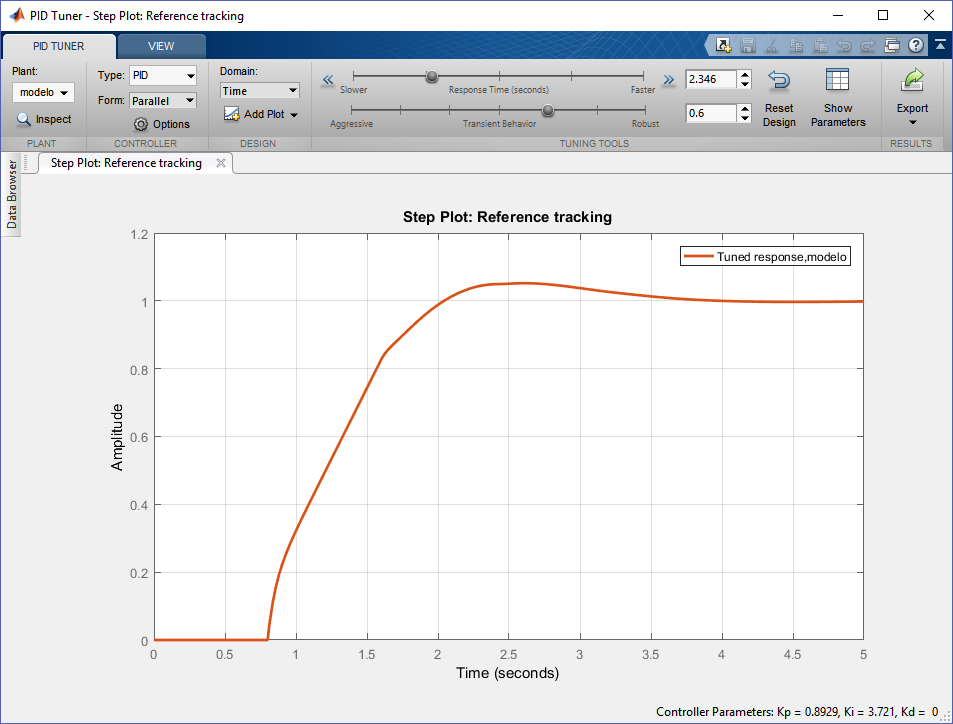
Cambiando el tiempo de respuesta (response time) podemos ajustar el comportamiento del sistema realimentado. En la figura anterior podemos ver en la esquina inferior derecha los coeficientes de los parametros del PID. En este ejemplo no se tiene un valor para el coefficiente Kd.

Estos coefficientes serán usados para hacer el control en lazo cerrado.

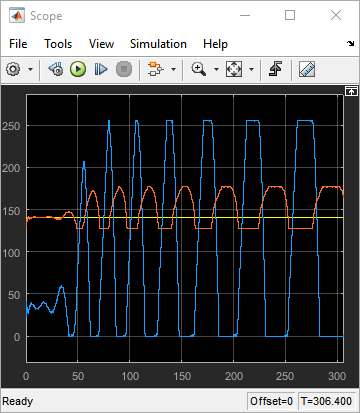
6. Verificación del Control en Lazo Cerrado

Para la verificación del control en el sistema real usaremos el archivo lazo_cerrado. Al igual que en la toma de datos se debe configurar el puerto de comunicación de la planta. Para acceder a estos bloques, se hace doble-clic en el bloque planta.

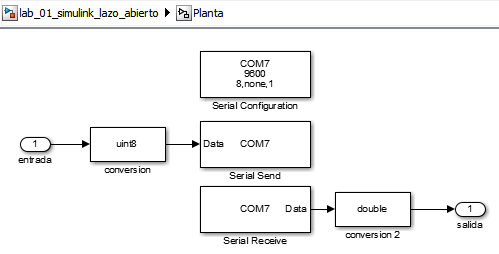
Si los parametros del controlador PID no son correctos se pueden obtener comportamientos inestables.